
*[Текст является переводом на русский язык статьи: , , . Standardized mean differences in meta-analysis: a tutorial. Cochrane Evid Synth Methods. 2024; 2:e12047. doi:10.1002/cesm.12047]
1. Введение
В этом руководстве основное внимание уделено стандартизированной разности средних (СРС-SMD) как показателю эффекта в мета-анализе. Мы объясним, что это такое, когда её следует использовать, как правильно вычислять и интерпретировать, а также некоторые из наиболее распространённых ошибок, допускаемых при синтезе доказательств.
Авторы обзоров используют СРС-SMD в качестве сводной статистики в метаанализе непрерывных исходов, когда все исследования оценивают один и тот же результат, но измеряют его с использованием множества различных шкал [1]. Например, мы можем взглянуть на метаанализ, в котором включённые исследования измеряли депрессивные симптомы своих участников с использованием различных шкал/опросников [2] (например, опросник депрессии Бека, гериатрическая шкала депрессии, рейтинговая шкала Гамильтона или Шкала депрессии Монтгомери-Асберга). Со статистической точки зрения практически невозможно напрямую количественно синтезировать результаты. Вместо этого решением было бы стандартизировать все эти данные с помощью общей меры размера эффекта: СРС-SMD (Рисунок 1).
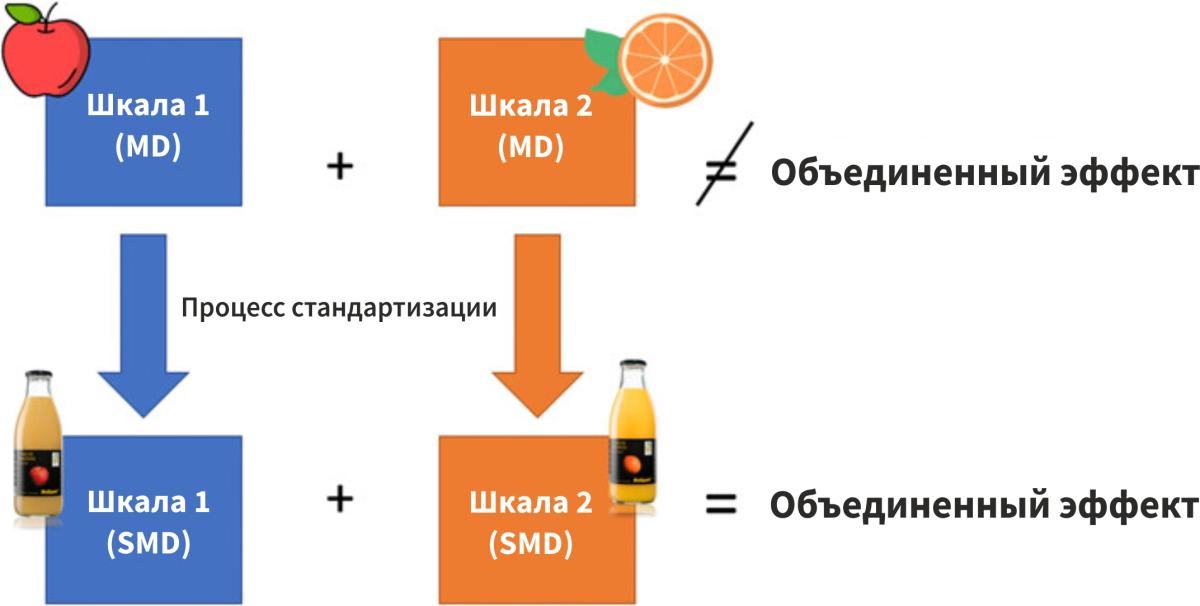
Как посчитать стандартизированную разность средних
Когда мы стандартизируем данные, мы делим разницу средних (РС-MD) между группой лечения и контрольной группой (т. е. величину эффекта лечения) на стандартное отклонение объединённой выборки (СОт-SD) в каждом исследовании (т. е. вариабельность показателей между участниками) измерения исходов, наблюдаемые в каждом исследовании) в один конкретный момент времени наблюдения [3]. Важно отметить, что разработчики обзора должны полностью детализировать эти процессы управления данными (например, стандартизацию данных), чтобы обеспечить прозрачность и воспроизводимость синтеза доказательств [3].
Расчет СРС-SMD с использованием стандартного отклонения (СОт-SD) объединённой выборки в определенный момент времени наблюдения.
Для лучшего понимания этой терминологии мы собираемся применить различные методы стандартизации к данным, полученным из опубликованного метаанализа [4]. Поэтому мы выбираем исследование Ортиса-Алонсо с соавт. [5], включённое в этот метаанализ, в котором были представлены результаты с использованием общего балла по шкале "Short Physical Performance Battery" (инструмент для оценки физической функции; SPPB) и извлекаем «сырые» данные (или необработанные, т. е. данные, непосредственно извлечённые из исследования без каких-либо преобразований) (Таблица 1).
Таблица 1. «Сырые» данные, извлеченные из исследования Ortiz-Alonso et al. [5] .
| Исследование | Шкала | Группа исследования | Исходный показатель | Показатель после лечения | ||||
|---|---|---|---|---|---|---|---|---|
| N | Средняя | SD | N | Средняя | SD | |||
Ortiz-Alonso et al. [5] | Краткий комплекс тестов физической активности (SPPB) | Лечение | 143 | 4 | 2.5 | 125 | 3.2 | 2.5 |
Контроль | 125 | 4.2 | 3.1 | 125 | 3.8 | 2.9 | ||
- Сокращения: N - размер выборки; SD - стандартное отклонение (СОт).
Затем, используя уравнение (1), мы стандартизируем эти данные при помощи объединённого стандартного отклонения исходов среди участников в контрольный момент времени наблюдения. Сначала мы рассчитываем стандартное отклонение для объединённой выборки (объединив группу лечения и контроля) дважды, для показателей исходного уровня и для показателей после лечения по уравнению (2).
Расчёт стандартного отклонения объединённой выборки. Суффикс «t» указывает на лечение, а суффикс «c» относится к ветви контрольной группы.
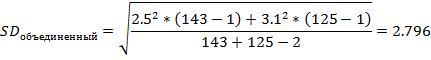
Стандартное отклонение объединённой выборки в контрольный момент времени наблюдения (для показателей после лечения):
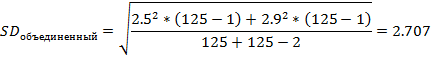
Затем мы преобразуем данные, основанные на ветвях исследования в "контрастные" данные (т. е. рассчитываем единый показатель эффекта, который показывает разницу средних РС-MD между двумя ветвями исследования), используя приведенные ниже уравнения. Попросту, мы вычитаем из средней группы лечения (Mt) среднюю группы контроля (Mc), то есть рассчитываем разность двух средних, лечения и контроля:
Вычисление РС-MD в контрольный момент времени наблюдения (после лечения), уравнение (3).
Расчет стандартной ошибки (СОш-SE) разницы средних (РС-MD) в контрольный момент времени наблюдения, уравнение (4) - SEMD.
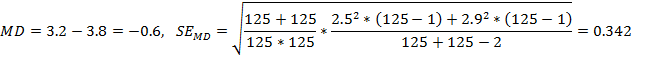
Затем мы стандартизируем наши MD и SE, разделив их на соответствующие стандартные отклонения объединенной выборки. Методологи поддерживают использование объединённых SD для показателей исходного уровня, а не для показателей последующих наблюдений (SD после лечения), но обычно в исследованиях сообщают только данные последующего наблюдения. Поэтому мы собираемся стандартизировать данные в обоих случаях: (1) предполагая, что у нас есть исходные данные, и (2) предполагая, что у нас есть только данные последующего наблюдения.
Стандартизированные данные (SMD и SE) с использованием SD объединённой выборки в контрольный момент времени наблюдения.
Хотя этот метод наиболее часто применяют в метаанализе, рекомендуется использовать специфичный относительно шкалы SD эталон [6, 7]. Более подробное объяснение этого метода можно найти у Gallardo-Gómez et al. [3] и в наших онлайн материалах.
3 Как интерпретировать Стандартизированную Разницу Средних
- Переосмысление СРС-SMD с помощью эмпирического правила для величины эффекта. Один из примеров которого, основанный на книге Коэна [8] выглядит следующим образом: 0.2 представляет собой небольшой эффект; 0.5 — умеренный эффект и 0.8 — сильный эффект. Тем не менее, некоторые методологи считают, что такие интерпретации проблематичны, поскольку важность результатов зависит от контекста и не поддается общим утверждениям [7].
- Преобразование СРС-SMD с помощью знакомого инструмента. Второй (рекомендуемый) вариант — перевыражение SMD в единицах одного или нескольких специфичных механизмов оценки. Этот метод может быть реализован путем умножения SMD на типичное SD для конкретной шкалы (например, сторонний эталон стандартного отклонения из большого когортного или поперечного исследования, которое соответствует целевой группе, внутренний эталонный SD или объединенный показатель SD), предпочтительно тот же, который используется для стандартизации данных [3]. Таким образом, используя исходные единицы шкалы, можно легче интерпретировать клиническую значимость и влияние совокупного эффекта лечения. В нашем примере, когда авторы объединили все размеры эффекта, они получили совокупный эффект лечения SMD = 0,40 (95% доверительный интервал: 0,02–0,77). Затем мы повторно выражаем этот размер эффекта в единицах SPPB, умножая на внешний эталон стандартного отклонения для исследуемой популяции (внешний эталон стандартного отклонения = 3,14), получая совокупный эффект для конкретного масштаба MD = 0,97 (95% ДИ: 0,06–2,42). Принимая во внимание заранее определенную минимально клинически значимую разницу в 1 балл по шкале SPPB [9] , мы могли бы поддержать использование вмешательства (физической активности в этом случае [4]) в конкретной популяции из-за его клинически значимой пользы для интересующего результата.
4 Распространённые ошибки при использовании Стандартизированной Разности Средних
- Ненужная стандартизация данных. Разработчикам системического обзора не нужно стандартизировать свои данные, если в оценке интересующего исхода не существует разных шкал. Убежденность в том, что термин «размер эффекта» является синонимом «SMD», может привести к тому, что авторы сообщат об эффекте лечения в SMD единицах, когда в этом нет необходимости. Одним из примеров этого является ситуация, когда на лесовидном графике сообщается только об одном исследовании; SMD не требуется, и эффект следует представлять в форме MD.
- Использование SE, а не SD для расчета SMD. Как мы видели в уравнении (1), мы используем SD объединенной выборки после обработки для расчета SMD. Тем не менее, первичные исследования могут ошибочно использовать оценку SE как SD или не указывать, сообщают ли они о SD или SE. Красным флагом для этого может быть довольно низкое стандартное отклонение (т. е. <1), хотя оно сильно зависит от диапазона оценок конкретной шкалы. Эта ошибка может привести к «раздуванию размера эффекта», поскольку, когда вы используете SE для расчета SMD, вы делите MD на меньшее значение относительно действительного значения параметра, тем самым получая более высокое значение. Поэтому, если вы получаете SMD больше единицы, вам следует проверить, использовали ли авторы исследования SD или SE.
- Смешение изменений относительно исходного уровня и разницы показателей эффекта после лечения. Хотя смешение изменений исходных показателей и результатов после лечения не является проблемой, когда речь идет о метаанализе MD [7], их в принципе не следует объединять с использованием SMD. Это связано с тем, что SD, используемые при стандартизации значений полученных после лечения, отражают вариабельность между людьми в один момент времени, тогда как SD, используемые при стандартизации оценок изменений, отражают различия в изменениях между людьми с течением времени, поэтому будут зависеть как от изменений в показателях у одного человека (в зависимости от продолжительности времени между измерениями), так и вариабельности в показателях между людьми [7].
- Направление размера эффекта. Существуют шкалы, в которых улучшение результата отражается снижением балла (например, в нашем иллюстративном примере: чем меньше времени затрачивается на прохождение дистанции, тем выше функциональная способность). Кроме того, чтобы интерпретировать величину эффекта, мы должны учитывать конкретный результат (например, более отрицательный эффект может быть положительным, если в обзоре исследуют симптомы депрессии, что означает уменьшение этих симптомов). Чтобы скорректировать эффект, который не соответствует направлению нашего метаанализа, мы должны умножить значение размера эффекта на –1 (никаких изменений для SD не требуется), гарантируя, что все эффекты имеют одно и то же направление.
- Нет интерпретации SMDs. Огромное число метаанализов часто оставляет оценки эффекта в виде SMD, что может затруднить интерпретацию. Выше мы говорили о различных доступных вариантах перевыражения SMD в более интерпретируемые оценки.
- Чтобы обеспечить воспроизводимость и прозрачность синтеза доказательств, предоставьте подробную информацию о направлении шкал и значениях размера эффекта, а также о методе, используемом для стандартизации и повторного выражения данных.
- Упростите интерпретацию результатов, повторно выражая объединенный эффект SMD в более знакомые единицы измерения для конкретной шкалы.
- Проверьте SMD, превышающий 1 SD, чтобы убедиться, что в анализ включены правильные данные.
5 Дополнительная информация
Когда мы упоминаем «размер эффекта» в этом руководстве и в Кокрейновских обзорах, в которых синтезированы стандартизированные разности средних, мы неявно имеем в виду размер эффекта, известный в социальных науках как g Хеджеса, который аналогичен размеру эффекта, называемому d Коэна с небольшой поправкой на смещение малой выборки. В этих величинах эффекта ( g Хеджеса и d Коэна) в знаменателе используют объединённое SD, которое представляет собой оценку SD, основанную на данных об исходах в обеих группах вмешательства, при условии, что SD в двух исследовательских группах аналогичны [7]. Напротив, другой размер эффекта, называемый дельтой Гласса (Δ) использует только SD из группы сравнения на том основании, что если экспериментальное лечение влияет на различия между людьми, то такое влияние лечения не должно влиять на оценку эффекта.
Все эти меры эффекта, называемые SMD, могут быть рассчитаны вручную или с помощью любого статистического пакета. Статистические пакеты в программном обеспечении R включают metafor [10], esc [11], или compute.es [12]. Полезным практическим ресурсом является bookdown за авторством Harrer et al., [13], который представляет собой доступное введение в то, как рассматривают метаанализы, включая различные расчеты SMD и методы объединения с примерами.
6 Дальнейшее чтение и онлайн контент
Больше информации о SMD можно найти в главе 6.5 Кокрейновского руководства по систематическим обзорам вмешательств [1].
Программа "Обучение Кокрейн" (Cochrane Training) разработала микро-обучающий модуль о том, как рассчитывать SMD, для дополнения к этой статье. (https://share.gomolearning.com/sharelink/b17d5bf8ee76fd1056d6a2505eb81375793889d0773d0141fd/) (Рисунок 2).

Вклад каждого из авторов
Даниэль Галлардо-Гомес: Концептуализация; написание — первоначальный черновик; написание — обзор и редактирование. Рэйчел Ричардсон: Руководство; написание — обзор и редактирование. Керри Дван: Концептуализация; руководство; написание — обзор и редактирование.
БЛАГОДАРНОСТИ
Авторы хотели бы поблагодарить Дарио Самбуньяка из директората по развитию Центрального исполнительного комитета Кокрейн, который спроектировал и создал модуль микрообучения, прилагаемый к этой статье.
Заявление о кофликте интересов
Рэйчел Ричардсон работает в Кокрейн. Керри Дван — бывший сотрудник Кокрейн. Другой автор заявляет об отсутствии конфликта интересов.
- , , . Chapter 6: choosing effect measures and computing estimates of effect. In: JPT Higgins, J Thomas, J Chandler, M Cumpston, T Li, MJ Page, VA Welch, eds. Cochrane Handbook for Systematic Reviews of Interventions. Cochrane; 2023: 143-176. Google Scholar
- , , , et al. Effect of exercise for depression: systematic review and network meta-analysis of randomised controlled trials. BMJ. 2024; 384:e075847. doi:10.1136/bmj-2023-075847 PubMedGoogle Scholar
- , , , , . Variability in meta-analysis estimates of continuous outcomes using different standardization and scale-specific re-expression methods. J Clin Epidemiol. 2024; 165:111213. doi:10.1016/j.jclinepi.2023.11.003 View PubMedWeb of Science®Google Scholar
- , , , et al. Optimal dose and type of physical activity to improve functional capacity and minimise adverse events in acutely hospitalised older adults: a systematic review with dose-response network meta-analysis of randomised controlled trials. Br J Sports Med. 2023; 57: 1272-1278. View PubMedWeb of Science®Google Scholar
- , , , et al. Effect of a simple exercise programme on hospitalization-associated disability in older patients: a randomised controlled trial. Geriat Med. 2019; 21(4): 531-537. doi:10.1101/19008151 Google Scholar
- , , , , . Meta-Analyses of Continuous Outcomes: Guideline Methodology Document 2. NICE Guidelines Technical Support Unit; 2021: 49. http://www.bristol.ac.uk/population-health-sciences/centres/cresyda/mpes/nice/guideline-methodology-documents-gmds/ Google Scholar
- , , , et al. Cochrane Handbook for Systematic Reviews of Interventions. John Wiley & Sons; 2019. View Google Scholar
- . Statistical Power Analysis for the Behavioral Sciences. 2nd ed. Erlbaum; 1998. Google Scholar
- , , , . Meaningful change and responsiveness in common physical performance measures in older adults. J Am Geriatr Soc. 2006; 54(5): 743-749. View CASPubMedWeb of Science®Google Scholar
- . Conducting Meta-analyses in R with the metafor package. J Stat Softw. 2010; 36: 1-48. View Web of Science®Google Scholar
- , , Calculator' from David BW. Package “esc”; 2017. Google Scholar
- . Compute.es: Compute Effect Sizes. R package version 0.2-2, 2013. https://cran.r-project.org/package=compute.es Google Scholar
- , , , . Doing Meta-Analysis with R: A Hands-On Guide. Chapmann & Hall/CRC Press; 2021. View Google Scholar
